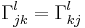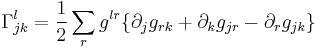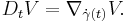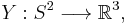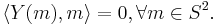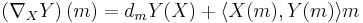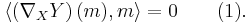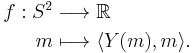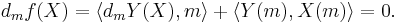Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle (an affine connection) preserving a given (pseudo-)Riemannian metric.
The fundamental theorem of Riemannian geometry states that there is a unique connection which satisfies these properties.
In the theory of Riemannian and pseudo-Riemannian manifolds the term covariant derivative is often used for the Levi-Civita connection. The components of this connection with respect to a system of local coordinates are called Christoffel symbols.
The Levi-Civita connection is named after Tullio Levi-Civita, although originally "discovered" by Elwin Bruno Christoffel. Levi-Civita,[1] along with Gregorio Ricci-Curbastro, used Christoffel's symbols [2] to define the notion of parallel transport and explore the relationship of parallel transport with the curvature, thus developing the modern notion of holonomy.[3]
The Levi-Civita notions of intrinsic derivative and parallel displacement of a vector along a curve make sense on an abstract Riemannian manifold, even though the original motivation relied on a specific embedding 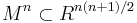 , since the definition of the Christoffel symbols make sense in any Riemannian manifold. In 1869, Christoffel discovered that the components of the intrinsic derivative of a vector transform as the components of a contravariant vector. This discovery was the real beginning of tensor analysis. It was not until 1917 that Levi-Civita interpreted the intrinsic derivative in the case of an embedded surface as the tangential component of the usual derivative in the ambient affine space.
, since the definition of the Christoffel symbols make sense in any Riemannian manifold. In 1869, Christoffel discovered that the components of the intrinsic derivative of a vector transform as the components of a contravariant vector. This discovery was the real beginning of tensor analysis. It was not until 1917 that Levi-Civita interpreted the intrinsic derivative in the case of an embedded surface as the tangential component of the usual derivative in the ambient affine space.
Contents |
Formal definition
Let 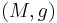 be a Riemannian manifold (or pseudo-Riemannian manifold). Then an affine connection
be a Riemannian manifold (or pseudo-Riemannian manifold). Then an affine connection 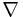 is called a Levi-Civita connection if
is called a Levi-Civita connection if
- it preserves the metric, i.e.,
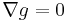 .
. - it is torsion-free, i.e., for any vector fields
 and
and  we have
we have ![\nabla_XY-\nabla_YX=[X,Y]](/2012-wikipedia_en_all_nopic_01_2012/I/a46e8900b1310f87838ba8dc11f1fa5f.png) , where
, where ![[X,Y]\,\!](/2012-wikipedia_en_all_nopic_01_2012/I/d45f1ae731f3bd438b85103fc03c862a.png) is the Lie bracket of the vector fields
is the Lie bracket of the vector fields  and
and  .
.
Condition 1 above is sometimes referred to as compatibility with the metric, and condition 2 is sometimes called symmetry, cf. DoCarmo's text.
Assuming a Levi Civita connection exists it is uniquely determined. Using conditions 1 and the symmetry of the metric tensor  we find:
we find:
By condition 2 the right hand side is equal to
so we find
Since  is arbitrary, this uniquely determines
is arbitrary, this uniquely determines 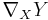 . Conversely, using the last line as a definition one shows that the expression so defined is a connection compatible with the metric, i.e. is a Levi Civita connection.
. Conversely, using the last line as a definition one shows that the expression so defined is a connection compatible with the metric, i.e. is a Levi Civita connection.
Christoffel symbols
Let 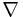 be the connection of the Riemannian metric. Choose local coordinates
be the connection of the Riemannian metric. Choose local coordinates  and let
and let 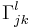 be the Christoffel symbols with respect to these coordinates. The torsion freeness condition 2 is then equivalent to the symmetry
be the Christoffel symbols with respect to these coordinates. The torsion freeness condition 2 is then equivalent to the symmetry
The definition of the Levi Civita connection derived above is equivalent to a definition of the Christoffel symbols in terms of the metric as
where as usual 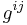 are the coefficients of the dual metric tensor, i.e. the entries of the inverse of the matrix
are the coefficients of the dual metric tensor, i.e. the entries of the inverse of the matrix 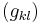 .
.
Derivative along curve
The Levi-Civita connection (like any affine connection) also defines a derivative along curves, sometimes denoted by  .
.
Given a smooth curve  on
on 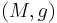 and a vector field
and a vector field  along
along  its derivative is defined by
its derivative is defined by
(Formally D is the pullback connection on the pullback bundle γ*TM.)
In particular, 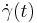 is a vector field along the curve
is a vector field along the curve  itself. If
itself. If 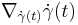 vanishes, the curve is called a geodesic of the covariant derivative. If the covariant derivative is the Levi-Civita connection of a certain metric, then the geodesics for the connection are precisely those geodesics of the metric that are parametrised proportionally to their arc length.
vanishes, the curve is called a geodesic of the covariant derivative. If the covariant derivative is the Levi-Civita connection of a certain metric, then the geodesics for the connection are precisely those geodesics of the metric that are parametrised proportionally to their arc length.
Parallel transport
In general, parallel transport along a curve with respect to a connection defines isomorphisms between the tangent spaces at the points of the curve. If the connection is a Levi-Civita connection, then these isomorphisms are orthogonal – that is, they preserve the inner products on the various tangent spaces.
Example
The unit sphere in 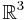
Let 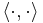 be the usual scalar product on
be the usual scalar product on 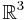 . Let
. Let 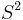 be the unit sphere in
be the unit sphere in 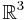 . The tangent space to
. The tangent space to 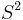 at a point
at a point  is naturally identified with the vector sub-space of
is naturally identified with the vector sub-space of 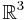 consisting of all vectors orthogonal to
consisting of all vectors orthogonal to  . It follows that a vector field
. It follows that a vector field  on
on 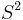 can be seen as a map
can be seen as a map
which satisfies
Denote by 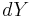 the differential of such a map. Then we have:
the differential of such a map. Then we have:
Lemma The formula
defines an affine connection on 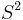 with vanishing torsion.
with vanishing torsion.
Proof
It is straightforward to prove that 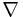 satisfies the Leibniz identity and is
satisfies the Leibniz identity and is 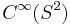 linear in the first variable. It is also a straightforward computation to show that this connection is torsion free.
linear in the first variable. It is also a straightforward computation to show that this connection is torsion free.
So all that needs to be proved here is that the formula above does indeed define a vector field. That is, we need to prove that for all  in
in 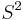
Consider the map
The map  is constant, hence its differential vanishes. In particular
is constant, hence its differential vanishes. In particular
The equation (1) above follows.
In fact, this connection is the Levi-Civita connection for the metric on 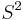 inherited from
inherited from 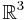 . Indeed, one can check that this connection preserves the metric.
. Indeed, one can check that this connection preserves the metric.
Notes
See also
References
Primary historical references
- Christoffel, Elwin Bruno (1869), "Über die Transformation der homogenen Differentialausdrücke zweiten Grades", J. für die Reine und Angew. Math. 70: 46–70
- Levi-Civita, Tullio (1917), "Nozione di parallelismo in una varietà qualunque e consequente specificazione geometrica della curvatura Riemanniana", Rend. Circ. Mat. Palermo 42: 73–205
Secondary references
- Boothby, William M. (1986). An introduction to differential manifolds and Riemannian geometry. Academic Press. ISBN 0-12-116052-1.
- Kobayashi, S., and Nomizu, K. (1963). Foundations of differential geometry. John Wiley & Sons. ISBN 0-470-49647-9. See Volume I pag. 158
- Spivak, Michael (1999). A Comprehensive introduction to differential geometry (Volume II). Publish or Perish Press. ISBN 0-914098-71-3.
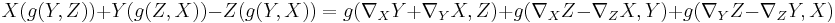
![2g(\nabla_X Y, Z) - g([X,Y], Z) %2B g([X,Z],Y) %2B g([Y,Z],X)](/2012-wikipedia_en_all_nopic_01_2012/I/55baa0c2eb386dca253c024e7b676244.png)
![g(\nabla_X Y, Z) = \frac{1}{2} \{ X (g(Y,Z)) %2B Y (g(Z,X)) - Z (g(X,Y)) %2B g([X,Y],Z) - g([Y,Z], X) - g([X,Z], Y) \}](/2012-wikipedia_en_all_nopic_01_2012/I/1ec3894d25b5f3ac1674cf5b53053bfd.png)